Higher, Faster, Stronger

The equations for motion in one dimension with constant acceleration are:

\(s=\frac{1}{2}(u+v)t\)

\(v=u+at\)

\(s=ut+\frac{1}{2}at^{2}\)

\(v^{2}=u^{2}+2as\)

Where \(s\) is displacement, \(u\) is initial velocity, \(v\) is final velocity, \(a\) is acceleration and \(t\) is time taken.

These equations are provided in the formulae booklet.

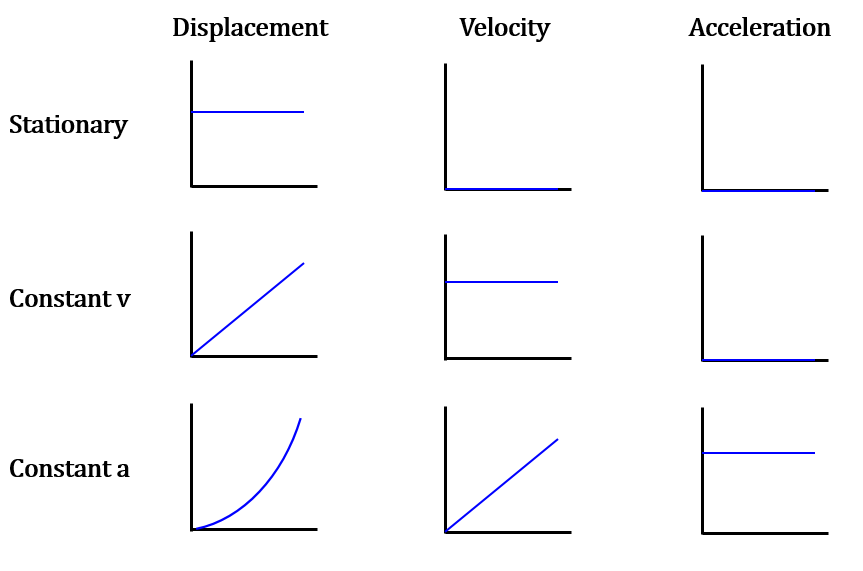
The gradient of a displacement-time graph gives the velocity.

The gradient of a velocity-time graph gives the acceleration.

The area underneath a velocity-time graph gives the displacement.

The area underneath an acceleration-time graph gives the velocity.

To estimate the area under a curved graph, you can count the number of squares.

A scalar quantity just has a magnitude, however a vector quantity has both a magnitude and a direction.

Examples of scalar quantities: mass, time, energy, temperature, distance, speed, etc.

Examples of vector quantities: force, displacement, velocity, acceleration, momentum, etc.

To resolve a vector is to split it into horizontal and vertical components.

One way you can do this is by drawing:

• Draw the vector to scale and in the correct direction.
• Draw a horizontal line from the tail and a vertical line from the tip of the vector to form a right-angled triangle.
• Measure the lengths of these lines, and use the scale to convert them.

Or, you can resolve a vector by calculation:

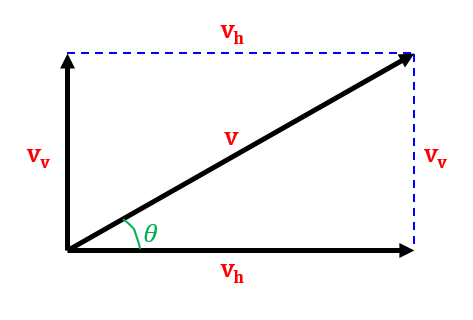
• \(v_{h}=v\cos\theta\)
• \(v_{v}=v\sin\theta\)

Weight (\(w\)) is the downward force on an object due to gravity.

\(w=mg\)

Where \(m\) is mass and \(g\) is the acceleration due to gravity.

Momentum (\(p\)) \( = mass \times velocity\).

Units \(=\) \(kgms^{-1}\).