Technology in Space

Current (\(I\)) is the rate of flow of charged particles.

\(I=\frac{Q}{t}\)

Where \(Q\) is charge and \(t\) is time.

Potential difference (\(V\)) is the energy transferred per unit charge.

\(V=\frac{W}{Q}\)

Where \(W\) is energy transferred and \(Q\) is charge.

Resistance (\(R\)) is a measure of how difficult it is to get a current to flow through a component.

\(R=\frac{V}{I}\)

Where \(V\) is the potential difference and \(I\) is the current.

Ohm's law states that current is directly proportional to potential difference, provided the temperature is constant.

\(V=IR\)

An Ohmic conductor is a conductor that obeys Ohm's law.

Charge cannot be created or destroyed - it is conserved. So, the charge entering a junction is the same as the the charge leaving it. Since current is the rate of flow of charge, the total current entering a junction is equal to the total current leaving it.

Energy cannot be created or destroyed - it is conserved. So, in a closed loop, the energy supplied to each coulomb of charge equals the sum of the energy transferred per coulomb of charge to each component. The total e.m.f. is equal to the sum of the potential differences across each component.

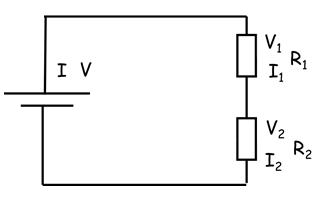
In a series circuit, the terminal p.d. is equal to the sum of the potential differences across each component.

\(V=V_{1}+V_{2}\)

\(V=IR\)

\(IR_{total}=I_{1}R_{1}+I_{2}R_{2}\)

In a series circuit, the current is the same at all points.

\(IR_{total}=IR_{1}+IR_{2}\)

\(R_{total}=R_{1}+R_{2}\)

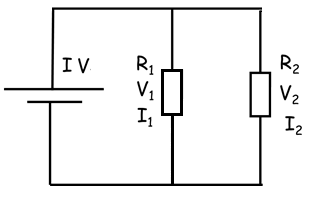
The sum of the currents entering a junction equals the sum of the currents leaving it.

\(I=I_{1}+I_{2}\)

\(I=\frac{V}{R}\)

\(\frac{V}{R_{total}}=\frac{V_{1}}{R_{1}}+\frac{V_{2}}{R_{2}}\)

The voltage in each branch of the circuit is the same.

\(\frac{V}{R_{total}}=\frac{V}{R_{1}}+\frac{V}{R_{2}}\)

\(\frac{1}{R_{total}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}\)

Power (\(P\)) is the rate of energy transfer.

\(P=W/t\)

\(P=IV\)

Where \(W\) is energy transferred, \(t\) is time taken, \(I\) is the current and \(V\) is the potential difference.

\(P=IV\)

\(V=IR\)

\(P=I\times IR\)

\(P=I^{2}R\)

\(P=IV\)

\(I=\frac{V}{R}\)

\(P=\frac{V}{R}\times V\)

\(P=\frac{V^{2}}{R}\)

E.m.f. (\(\mathcal{E}\)) is the energy supplied per coulomb of charge.

Internal resistance (\(r\)) is the resistance of the power supply.

Terminal potential difference (\(V\)) is the potential difference measured across the terminals of the power supply.

The lost volts (\(Ir\)) is the energy transferred per unit charge as heat to the surroundings due to the internal resistance of the power supply.

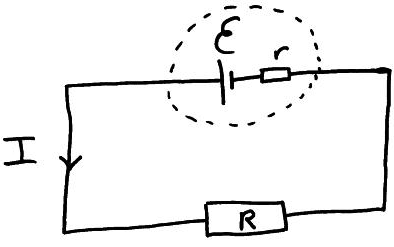
\(\mathcal{E}=V+Ir\)

\(\mathcal{E}=I(R+r)\)

Metals consist of a sea of delocalised electrons in a lattice of positive ions.

Heating the metal causes these ions to vibrate more, causing the electrons to collide with the ions more frequently, transferring some of their kinetic energy into other forms, making it more difficult for the electrons to flow.

Intensity (\(I\)) is the rate of energy transfer per unit area at right angles to the direction of travel of the wave.

\(I=\frac{P}{A}\)

Where \(P\) is power and \(A\) is area.